仿真结果共享在Mathematica中的实现

该文不包含实现过程，仅介绍Mathematica中的仿真结果共享的方案，作为这篇文章的一个辅助材料。

Mathematica在仿真数据上的处理方法是相当优雅的，这个解决方案是InterpolatingFunction。这种函数的表现方式和正常的函数几乎相同，你可以对它求值、求导、求积分等等等等。可能不是对于所有问题，这个方案都能获得最好的结果，但是应该说对于大部分问题这个函数的表现还是比较不错的。Mathematica中有不少函数可以返回InterpolatingFunction，诸如Interpolation, FunctionInterpolation, NDSolve等等。这里举个NDSolve的例子吧！

考虑单自由度弹簧质量系统的自由振动问题，其控制方程为：

\begin{equation} m \ddot{x} + c\dot{x} + k x = 0
\end{equation}

假设初值条件为：

\begin{equation} x(0)=1
\end{equation} \begin{equation} \dot{x} (0)=0 \end{equation}

假设上述问题的$m=1$, $k=100$, $c=0.1$， 那么求解这个方程的标准Mathematica代码应该是：

 disp[t_] = 
  x[t] /. NDSolve[{x''[t] + 1/10 x'[t] + 100 x[t] == 0, x[0] == 1, 
     x'[0] == 0}, x[t], {t, 0, Pi}];

这样你就得到了一个InterpolatingFunction disp[t]，对于这个函数你可以求值，可以绘图，可以求导，可以积分，比如：

Plot[disp[t], {t, 0, Pi}]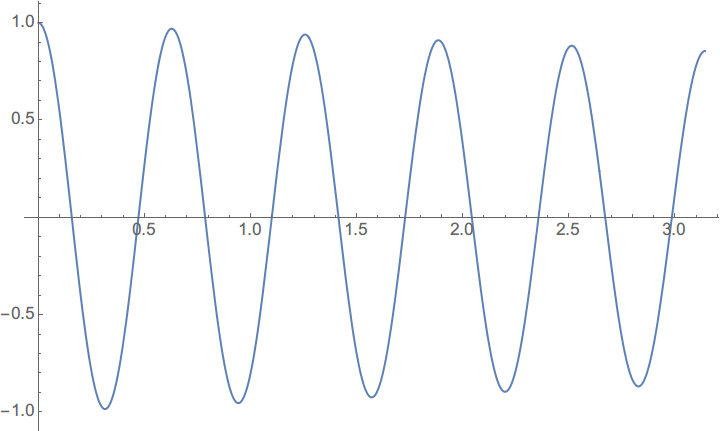

Plot[disp'[t], {t, 0, Pi}]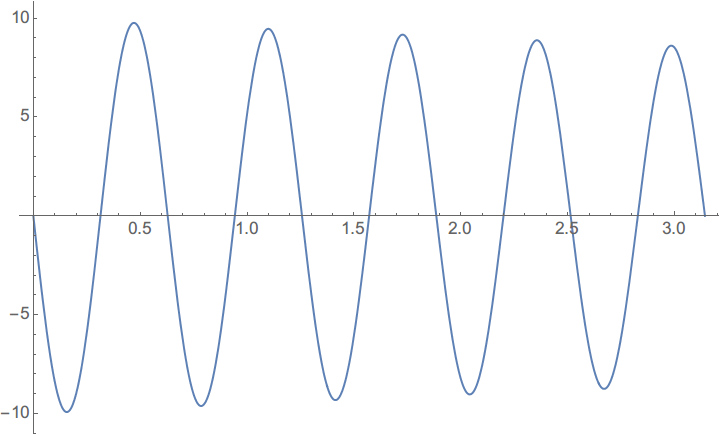

Plot[disp''[t], {t, 0, Pi}]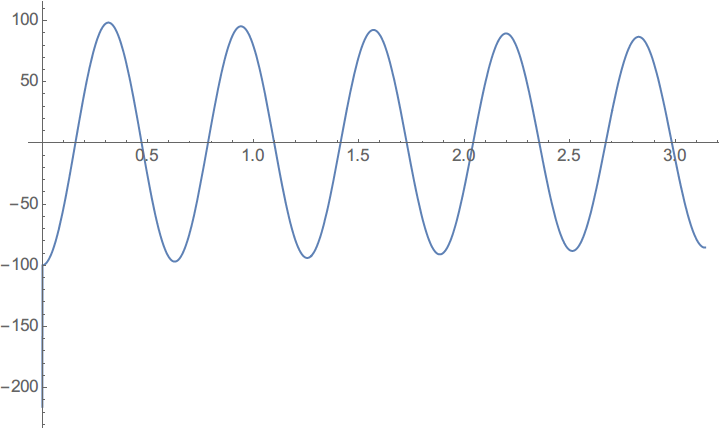

可以看到除了起始点边界处加速度稍有跳跃，其他位置都比较理想。

NIntegrate[disp[t]^2, {t, 0, Pi}]
>> {1.34811}

如果你到这还要问这和仿真结果有什么关系呢，那好吧，就看看仿真结果吧。

首先仿真出点数据：

x = Range[0, 100, 5];
y = (x + RandomReal[1, Length[x]])^2 + 
  Sin[x + RandomReal[1, Length[x]]];
  Transpose@{x, y} // ListPlot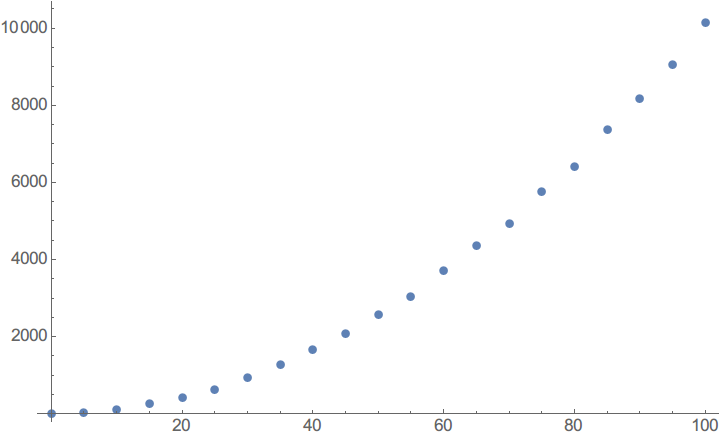

然后插值，这里直接用默认插值方法了

f = Interpolation[Transpose@{x, y}];
Plot[f[t], {t, 0, 100}]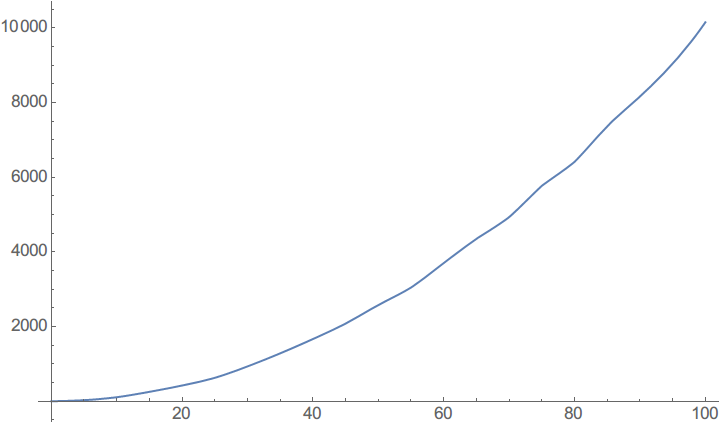

可以看到，数据中的随机误差同样被表示出来了，所以这个函数是有能力表现出一些仿真中的细节变化的。下面展示一下对于这个函数的积分，可以预想对于高斯噪声的积分将会被抵消，所以积分曲线应该比原曲线光滑得多。

Plot[NIntegrate[f[t], {t, 0, x}], {x, 0, 100}]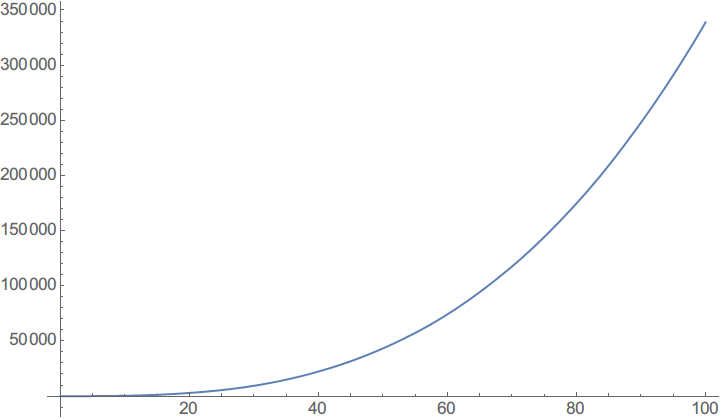

下面给一个跟我研究有关系的例子吧，假设我们仿真获得的数据是这样的：

x = Range[0, 100, 5]
y = (x + RandomReal[1, 
      Length[x]] (UnitStep[x - 20] - UnitStep[x - 40]))^2

也即认为这个函数在x从20到40有一个小的随机扰动，我们试图使用曲率的方式把它识别出来。

首先，函数的曲线本身看起来还是比较光滑的

f = Interpolation[Transpose@{x, y}]
Plot[f[t], {t, 0, 100}]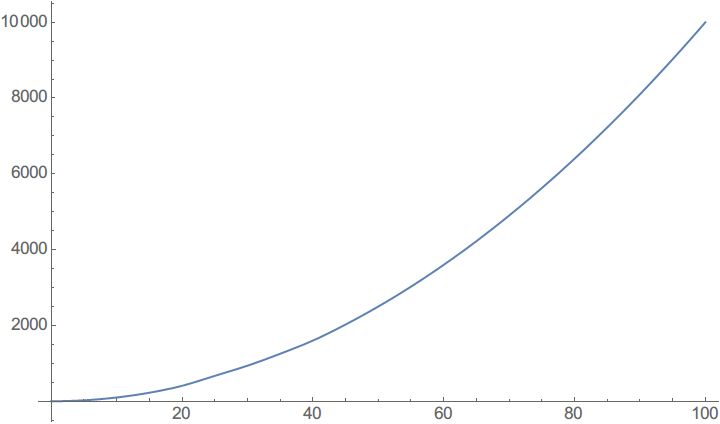

求函数的二阶导，可以看到二阶导数在添加噪声的区段有很明显的提高，这就是曲率模态检测损伤的基本想法。

Plot[f''[t], {t, 0, 100}, PlotTheme -> "Monochrome", 
 PlotRange -> All, GridLines -> {{20, 40}, {}}]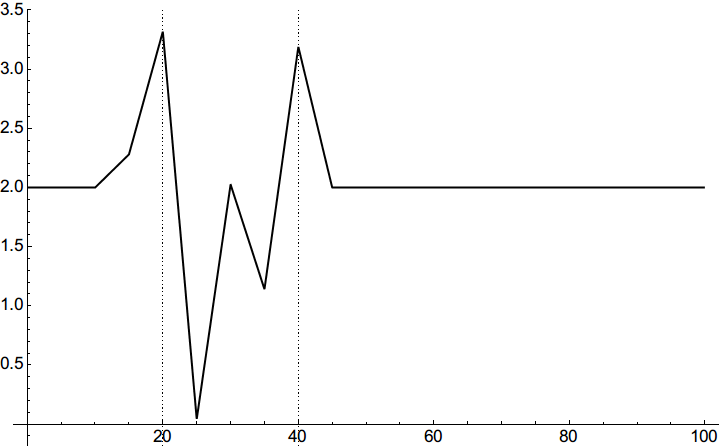

综上所述，共享InterpolatingFunction完全可以高精度的分享仿真的结果，没有必要通过拟合公式的方法，而且InterpolatingFunction可以提供几乎所有拟合公式可以提供的功能。当然，这只是分享仿真数据的一种方法，而且要在其他环境下实现这个功能并没有太大的困难，所以我还是认为没有必要再为了获得所谓的“公式”去拟合仿真结果。