啃老中复利有多重要?
2016年04月04日 数学 就业 社会 行 添加评论早先乙寅发了一个文章提到算不算利息,收益可能有很大区别,而且特别提到复利是相当厉害的!这是相当正确的。不过在一定条件下,情况并不是这样。
对于乙寅报纸里提到的情况,仅计算单次利息的计算结果和计算复利的计算结果差异并没有想象得大。下面是具体实现:
total = input +
Sum[(input - i salary) monthrate, {i, 0, input/salary}]
> input + (input monthrate (input + salary))/(2 salary)input 是输入资本量,salary是每月取出资本量,monthrate是月利率。
按照一样的月利率计算定义(这样算出来的月利率,无法还原得到年利率。可以还原的算法,参见文章最后的算法。)
monthrate = (yearrate + 1)^(1/12) - 1;那么,输入的资金大概可以花的年数是:
n1 = total/salary/12
> (input + (input (input + salary) (-1 + (1 + yearrate)^(1/12)))/(
2 salary))/(12 salary)对于计算复利的情况,这个时间长度是:
n2 = n/12 /.
Quiet@Solve[
input (1 + monthrate)^n ==
Sum[salary (1 + monthrate)^i, {i, 0, n - 1}], n]
> {-(Log[((1 - (1 + yearrate)^(1/12)) (input + salary/(
1 - (1 + yearrate)^(1/12))))/salary]/Log[1 + yearrate])}对于报纸中使用的那个算例,计算单次利息和复利,可以使用的年限分别是:
{n1, n2} /. {input -> 100, salary -> .5, yearrate -> 0.03}
> {20.7977, {22.9964}}也就是差不多两年的差异。然而,如果你认为乙寅的看法是错误的,那么你就太低估复利的作用了。
对于文中算例的情况,如果年利率高一点,你就会得到下面的曲线:
Plot[Evaluate[{n1, n2} /. {input -> 100, salary -> .5}], {yearrate,
0.01, 0.1}, PlotLegends -> {"n1", "n2"}, GridLines -> Automatic,
PlotTheme -> "Web"]可以看到,如果年利率涨到5%,这两种方法的计算结果就已经相差一倍了。超过6%,单次利率能够使用的年数就完全是无穷小量了。其实如果你初始本金多一点点,也会是完全不同的情况,比如我们初始本金仅仅大50%,也就是150万,那么你得到的曲线是这样的。
Plot[Evaluate[{n1, n2} /. {input -> 150, salary -> .5}], {yearrate,
0.01, 0.1}, PlotLegends -> {"n1", "n2"}, GridLines -> Automatic,
PlotTheme -> "Web"]为了充分的展示这种区别,假定月入不变,那么可以得到下面的三维图:
Plot3D[Evaluate[{n1, n2} /. {salary -> .5}], {yearrate, 0.01,
0.1}, {input, 50, 200}, PlotLegends -> {"n1", "n2"},
MaxRecursion -> 5, PlotTheme -> "Detailed", ImageSize -> Large]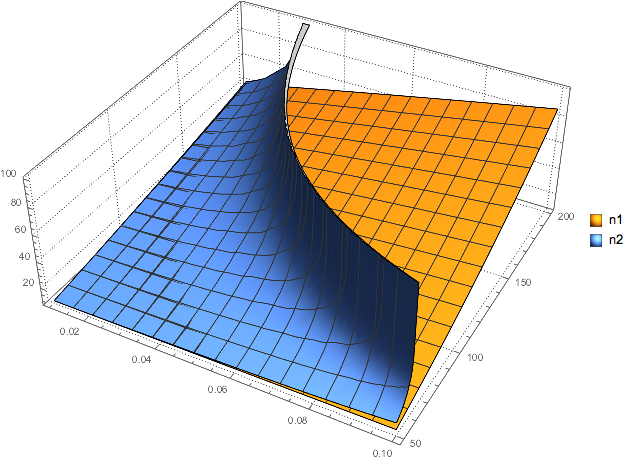
可以看到利率越高,本金越大,那么最后的结果也就差别越大。复利的作用在每月输出量比利息多不太多的情况下才会发挥出巨大的作用,如果这两种差别较大那么两种的差异就并不显著了。
单次利率的问题
上面的单次利率情况下,月利率累计是不能得到年利率的,因为刚才的表达式月利率是计算复利的。如果不计算复利,要得到年利率,那么每个月的利息就是年利率的1/12。那么就有以下的结果:
n12 = With[{monthrate = (yearrate/12)},
Evaluate[total/salary/12]]
> (input + (input (input + salary) yearrate)/(
24 salary))/(12 salary)对于文中算例,这种算法的使用年限大概是:
{n1, n12, n2} /. {input -> 100, salary -> .5, yearrate -> 0.03}
> {20.7977, 20.8542, {22.9964}}结果与计算复利差别并不大,这个结果可以推广到一般的情况。
输入本金100万的情况是这样的:
Plot[Evaluate[{n1, n12, n2} /. {input -> 100,
salary -> .5}], {yearrate, 0.01, 0.1},
PlotLegends -> {"n1", "n12", "n2"}, GridLines -> Automatic,
PlotTheme -> "Web"]输入本金150万的情况是这样的:
Plot[Evaluate[{n1, n12, n2} /. {input -> 150,
salary -> .5}], {yearrate, 0.01, 0.1},
PlotLegends -> {"n1", "n12", "n2"}, GridLines -> Automatic,
PlotTheme -> "Web"]可以看到确实这样计算能够多一些年份,不过这种差异对于计不计算复利来讲基本上可以忽略不计。




