$\mathrm{sinc}(x)$在$[0,+\infty)$不绝对可积的证明

sinc 函数的定义是：

\begin{equation} \mathrm{sinc} x = \frac{\sin{\pi x}}{\pi x} \end{equation}

容易知道，$|\mathrm{sinc}(x)|\le \mathrm{sinc}(0) = 1$（根据洛必达法则），所以它属于 $\mathcal{L}^{\infty}$。但其1范数为：

\begin{equation} \int_{-\infty}^{\infty}|\mathrm{sinc}(x)| dx = 2 \int_{0}^{\infty} \frac{|\sin{\pi x}|}{|\pi x|} dx \end{equation}

然而上式是发散的。可以像这样证明这一结论：

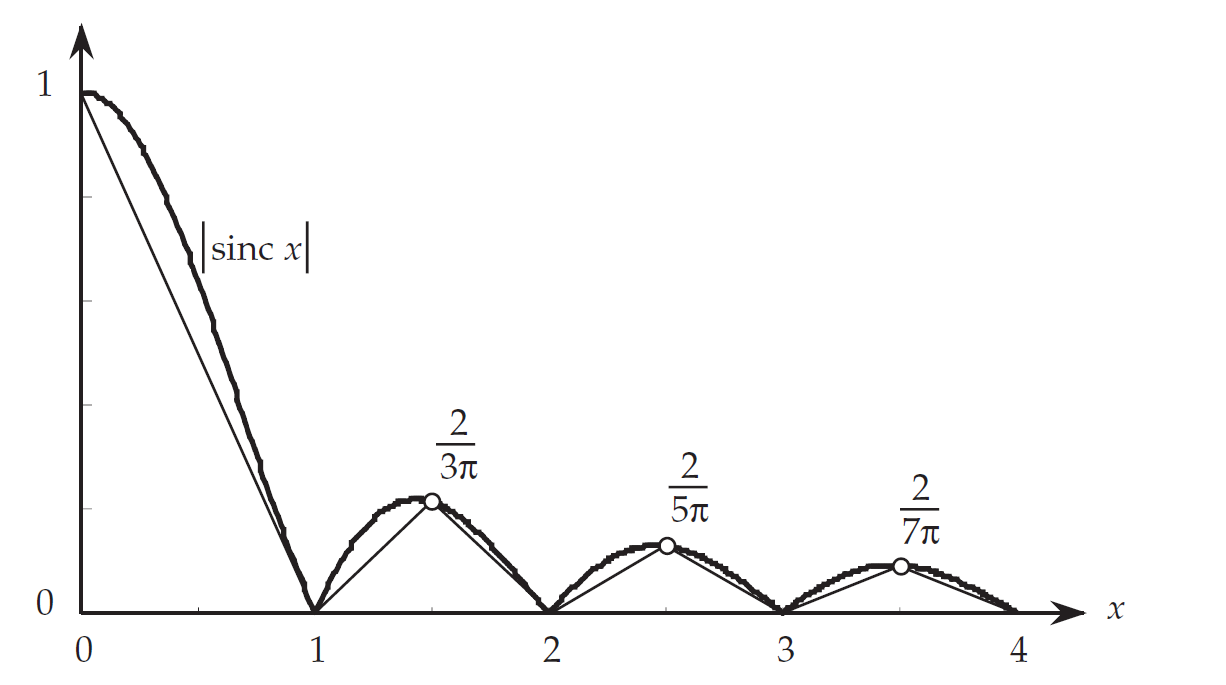
构造如图所示的一个函数，它处处小于等于 sinc，但是它的一范数发散。显然，当$x$在0到1之间， $|\mathrm{sinc}(x)|$下包围的面积大于下面面积为1/2的三角形面积；对于之后的任意一个区间$(k,k+1)$，都有$|\mathrm{sinc}(x)|$下包围的面积大于高为$\frac{|\sin{\pi (k + 1/2)}|}{|\pi (k+1/2)|} = \frac{1}{\pi (k+1/2)} $，也即三角形的面积为$I_k = 1/\pi (2k+1)$。

由于函数的1范数的下界为三角形面积和

\begin{equation} \lVert\mathrm{sinc}\rVert_1>2\left(\frac{1}{2}+\sum_{k=1}^{\infty}I_k\right)=1+\frac{2}{\pi}\sum_{k=1}^{\infty}\frac{1}{2k+1} \end{equation}

发散，所以函数的1范数必发散。